How can you estimate the cut angle for a shot?
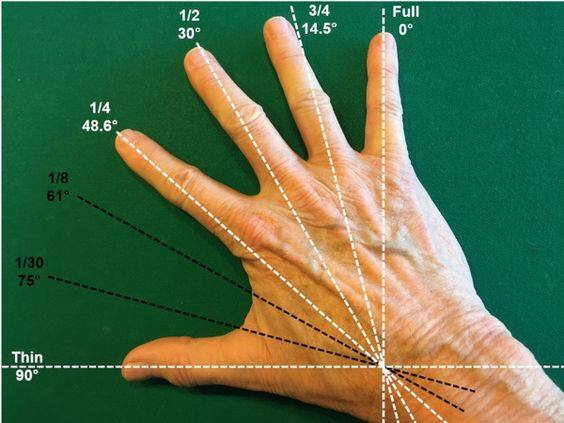
On Vol. I of the Video Encyclopedia of Pool Shots, we show how to use your hand to recognize 1/4-ball, 1/2-ball, and 3/4-ball hits. We also show how to calibrate your hand so you can judge these shots (and the corresponding cut angles) fairly accurately. Knowing these three angles well can help you estimate the angle required for any shot. “HAPS – Part I: Fractional-Ball Aiming” (BD, November, 2014) also has diagrams and illustrations that help you visualize and practice standard ball-hit fractions. The cut angles for various ball-hit fractions can be found at the end of TP A.23.
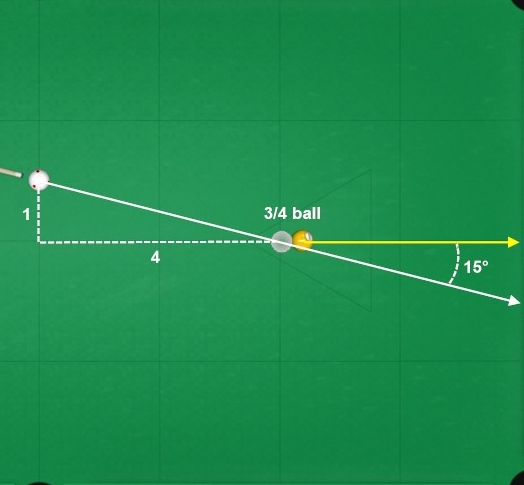
A simple way to visualize and estimate cut angles is to imagine an analog clock face (or use one on your wrist). If noon (12) is straight (0°), 11 and 1 are at 30° (1/2-ball hit), 10 and 2 are at 60° (about an 1/8-ball hit), and each minute is 6°. For example, halfway between 12 and 1 ( at 2 1/2 minutes) is 15° (about a 3/4-ball hit), and halfway between 1 and 2 is 45° (about a 1/4-ball hit).
Other methods for visualizing cut angles can be found on the fractional-ball aiming resource page. Here’s a diagram from Patrick Johnson illustrating the where the ball-hit fractions are relative to clock hours:
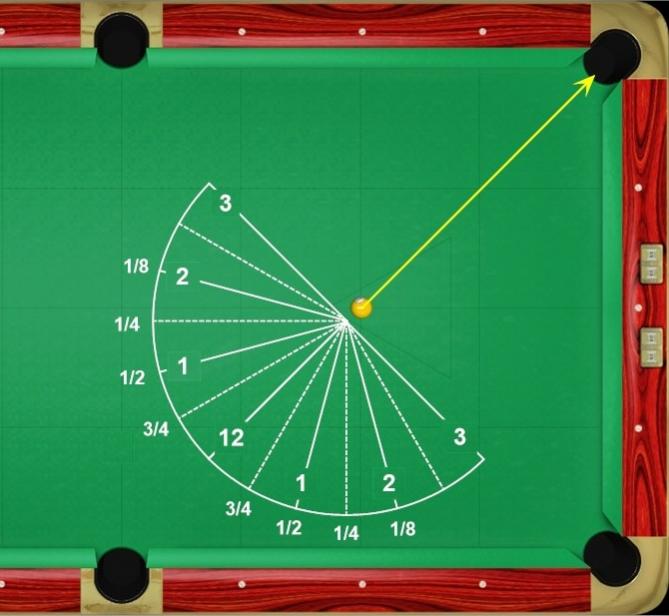
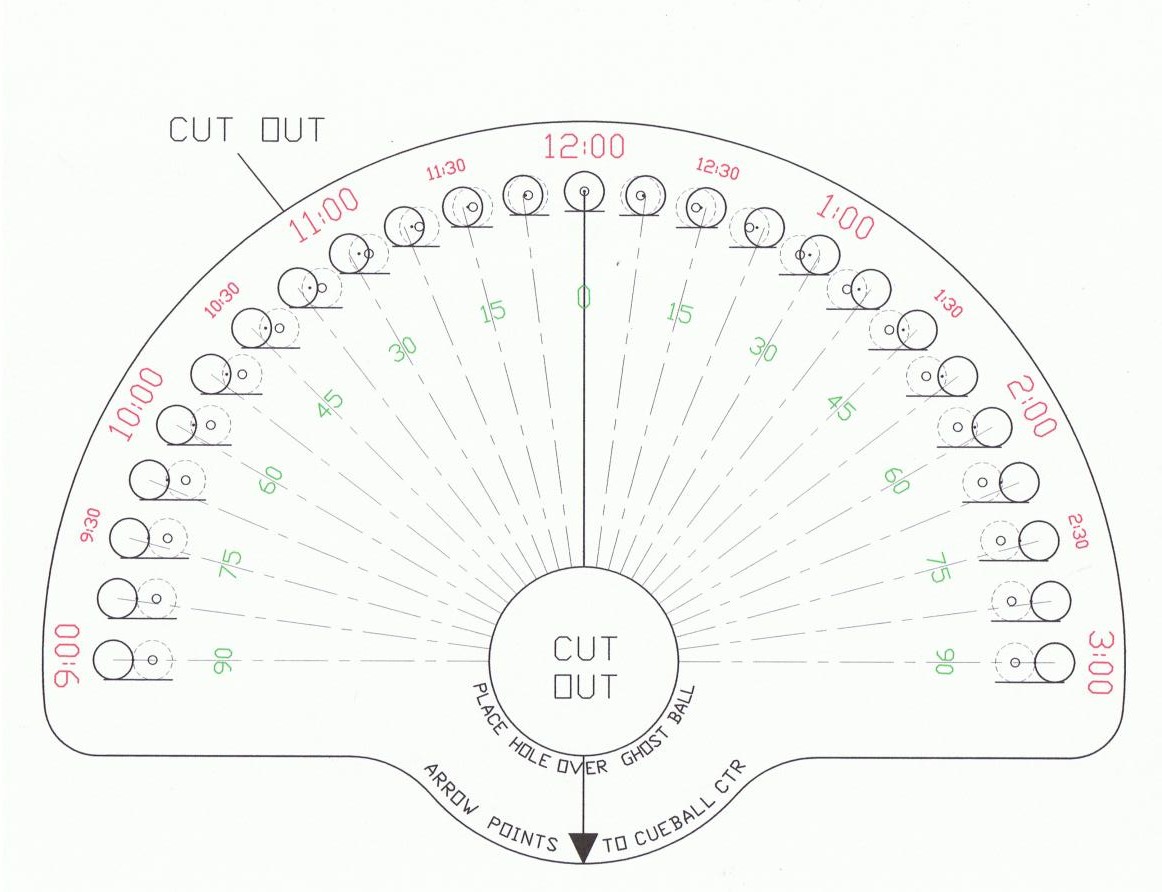
Below is a template from Dan Traylor (from “oldschool1478” in AZB post) that can be useful to estimate cut angles and required aim points when practicing. Here’s a printable PDF version. If the center of the cutout is placed over the necessary ghost-ball position with the arrow pointed back to the cue ball, sighting to the pocket gives the necessary cut angle, clock position, ghost-ball overlap, and aim point (center of small circle) relative to the object ball. For example, the required aim for a 30° cut (assuming no throw) is through the edge of the object ball. The dashed ghost-balls in the small illustrations are useful to get a sense for the amount of ball overlap required on a particular shot.
AimPro Billiards has a similar easy-to-use plastic template and system called AimRight that can be used to estimate cut angles, ball-hit fractions, and CB directions. CueAndMe also has useful templates and a system for estimating cut angles by visualizing rectangles of different proportions.
from Patrick Johson (in AZB post):
1-to-1 slope = 45-degree cut = 1/4 ball fraction
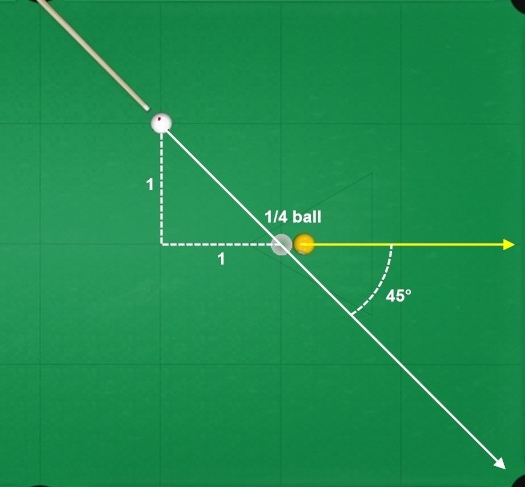
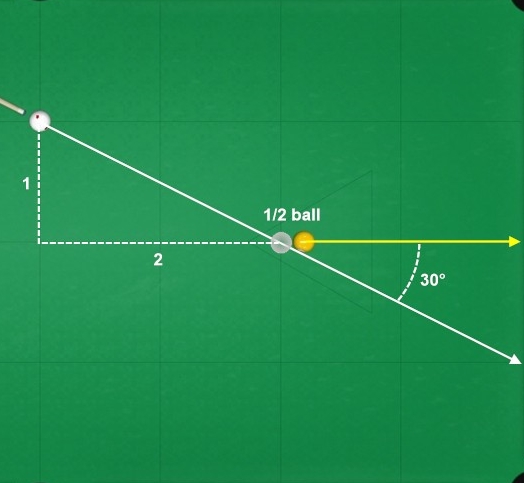
1-to-2 slope = ~30° cut = ~1/2 ball fraction
[Actual: 1.15-to-2 slope = 30° cut]
1-to-4 slope = ~15-degree cut = ~3/4 ball fraction
[Actual: 1.07-to-4 slope = 15° cut]
from Patrick Johnson:
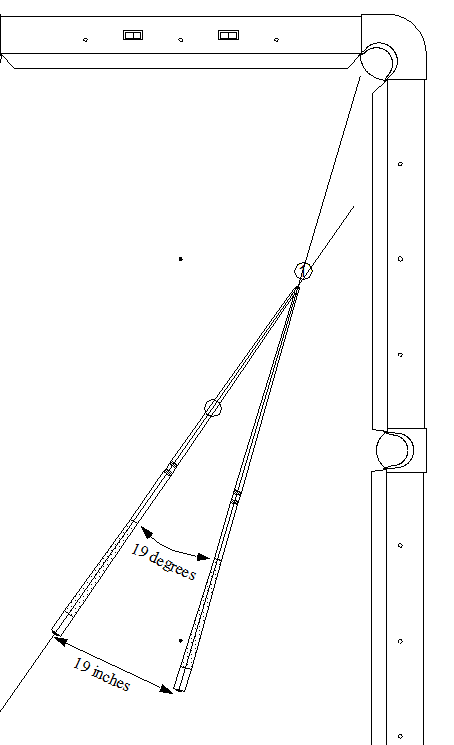
from Bob Jewett (in AZB post):
If you place your tip at the center of the ghost ball and pivot around it from the line to the pocket to the line of the shot (over the cue ball), the number of inches the bumper on the cue travels is the number of degrees of the cut angle.
To be precise, you should measure the distance around the arc of the travel of the bumper, but for cut angles up to 30 degrees the straight-line distance between the two positions of the bumper is pretty close.
The tip of the cue is at the center of the ghost ball. The distance X is the base of an isosceles triangle. If X is measured in quarter inches, it gives the angle, pretty nearly.
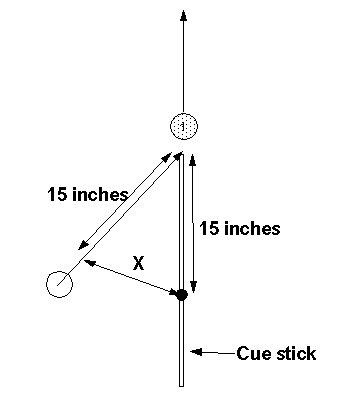
Here are x (in) x (in/4) actual angle and error:
1 4 3.82 0.18
2 8 7.65 0.35
3 12 11.48 0.52
4 16 15.32 0.68
5 20 19.19 0.81
6 24 23.07 0.93
7 28 26.99 1.01
8 32 30.93 1.07
9 36 34.92 1.08
10 40 38.94 1.06
11 44 43.02 0.98
12 48 47.16 0.84
13 52 51.36 0.64
14 56 55.64 0.36
15 60 60.00 0.00
16 64 64.46 -0.46
17 68 69.04 -1.04
18 72 73.74 -1.74
19 76 78.59 -2.59
from Dead Crab:
I have a way of estimating cut angles to within a degree. It works for me. Estimating to within 5° would be a cinch.
1. Place a small piece of tape (blue painter’s tape is good) on your cue shaft 15″ from the tip
2. Place tip of cue on the CB-OB line so that the 15″ mark on the cue is over the top of the CB (obviously, not touching it).
3. Leaving the tip stationary, swing the butt of the cue so that the alignment of the cue long axis is parallel to the line of the OB-intended pocket.
4. Estimate the distance (in inches) from the tape mark on the cue to the CB-OB line (i.e. drop a perpendicular to the CB-OB line from the mark on the cue. Multiply this distance by 4. That is your cut angle, in °.
With a little practice, the difference between 3.5″ and 4″ is obvious, and clearly distinguishes a 14 degree from a 16 degree cut angle. For longer shots, you can use the cue joint rather than the 15″ mark, and multiply by 2 instead of 4 to get the cut angle.From a practical viewpoint, it is important to note that the tip of the cue need not be at the GB center. Since the GB center may be 7′ away, a more practical approach is to place the 15″ mark on your cue over the CB, with the tip on the estimated CB-GB line (as discussed, for long shots the CB-OB line is often adequate for longer shots). Then pivot the cue around the tip until it lies parallel to the OB-pocket line. Estimate the base of the triangle in inches, multiply by 4, and you are done. For really close shots the method can be used by extending the estimated CB-OB line “behind” the CB. This saves a lot of reaching. For intermediate and long shots, the 30″ point of the cue is often easiest to use (just 1″ above joint), and then the multiplier is 2 instead of 4.
If you know the cut angle, you know where to aim from the CB center. 1mm per degree up to 30° and above that, 0.8mm/degree off ball edge over 30° covers it pretty well. Ball landmarks come in handy. A visible gap becomes apparent between cloth and ball at about 10mm off center (napped), 7-8 mm worsted. A 20 degree cut can be aimed at 7:30 or 4:30 on the clock face, a 25 degree shot at 8:00 or 4:00. A 23 degree cut is 2mm shy of a 25 and 3mm more than a 20.
from Zafer Barutcuoglu (via e-mail):
Here’s a system for using the diamonds to approximate angles among the CB, OB, and pocket to determine the required throw-adjusted cut angle and and ball-hit fraction for any shot:
Dr. Dave keeps this site commercial free, with no ads. If you appreciate the free resources, please consider making a one-time or monthly donation to show your support:
