Are fixed-line of aim, fractional-ball aiming systems useful?
Fractional ball aiming is illustrated and described in the following videos, the first from Vol. I of How to Aim Pool Shots (HAPS):
and in part 2 of NV B.3 – Mike Page’s aiming video (part 1, part 2). For more info, see: “HAPS – Part I: Fractional-Ball Aiming” (BD, November, 2014).
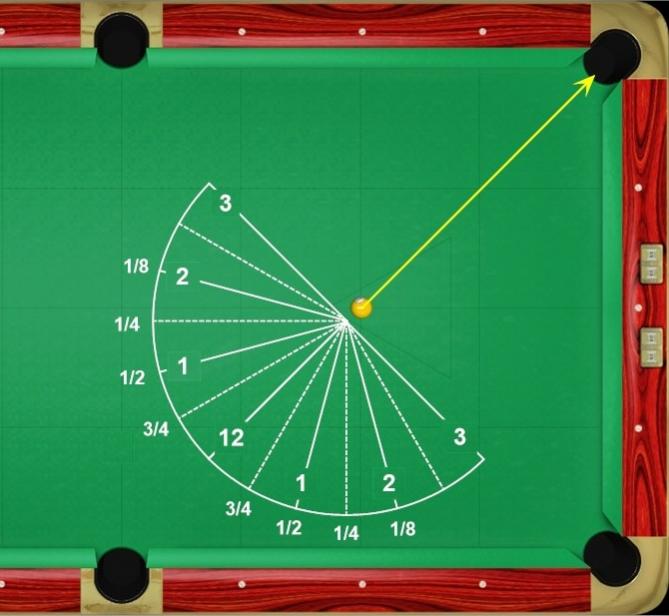
Also, here’s a useful illustration from “Aim, Align, Sight – Part I: Introduction and Ghost Ball Systems” (BD, June, 2011) defining the standard ball-hit fractions:
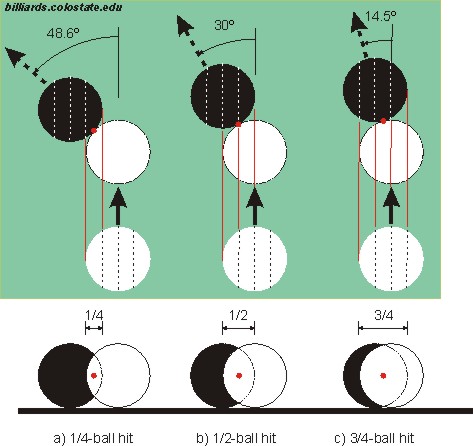
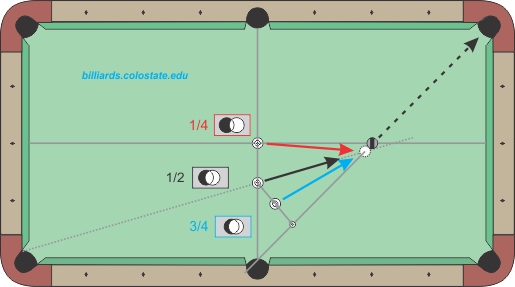
And here are ball layouts one can use to set up the standard ball-hit fractions at a table (from “HAPS – Part I: Fractional-Ball Aiming” – BD, November, 2014, and “Aim, Align, Sight – Part I: Introduction and Ghost Ball Systems” – BD, June, 2011):
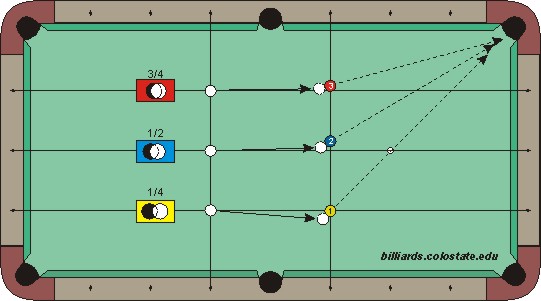
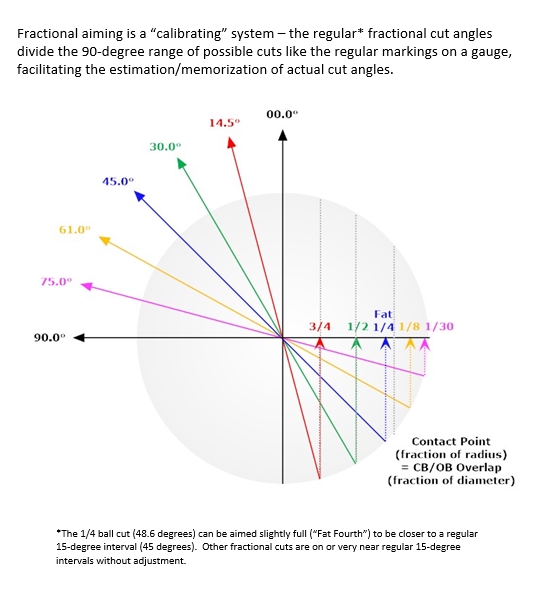
The illustrations below (from Patrick Johnson) show the approximate cut angles for all standard ball-hit fractions. For more information on how ball-hit-fraction is related to cut angle, see the ball-hit fraction vs. cut angle resource page. TP A.23 – Ball-hit fraction vs. cut angle shows equations and plots for all ball-hit fractions and cut angles. See estimating cut angles and below for other methods to visualize fractional-ball cut angles.
The 1/2-ball hit has many useful applications when playing pool, as demonstrated in the following videos:
Various aiming systems (even though they are not perfect) do help some people aim, concentrate, focus on the OB, stay down, and shoot better. I don’t think anybody (even me) would say that is a bad thing. On the other hand, people should realize that fixed-point aiming systems with a limited number of aiming lines are not perfect and will cause you to miss shots if you don’t compensate (consciously or subconsciously).
The common fractional-ball aiming system, sometimes referred to as Hal Houle’s 3-angle system. Basically, the claim is there are only three different aims for all cut shots: a “15° cut,” a “30° cut,” and a “45° cut.” In TP A.11, I show that these aims are equivalent to 3/4-, 1/2-, and 1/4-ball-hits and the 15- and 45° angles are not exact. Also, I show an example shot “in between” two of the aim references to show a deficiency of the method. The method provides easy visual aiming, and it helps a player establish good reference aims for different ranges of cut shots; but for “in-between” cut angles, one must adjust or compensate between the aim references.
Fractional-ball aiming references (1/4, 1/2, and 3/4), on either the CB or OB, can be useful to help some people aim because the references are easy to visualize. However any system that offers only a limited number of lines of aim from which to choose can be limiting if the user isn’t good at adjusting for the many shots that fall between these references. For more info, see: limited lines or alignments of aim. Also, any “aiming system” can offer a person benefits, especially a person that doesn’t aim accurately or consistently.
from Patrick Johson (in AZB post):
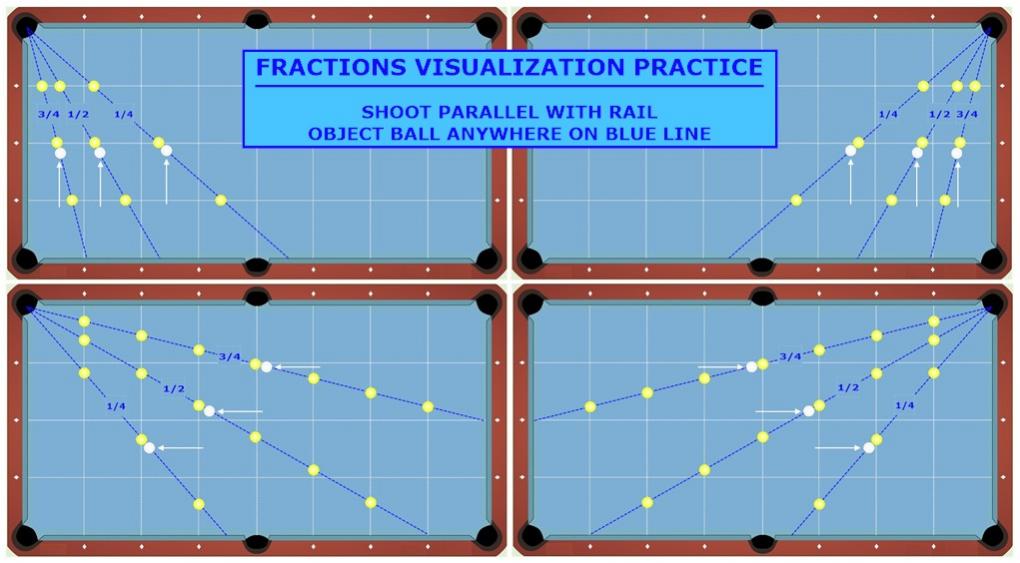
Per the diagram below, place an object ball anywhere on one of the lines (near or far from the pocket) and shoot the CB parallel with the long rails, aiming at the fraction shown for that line. Sighting the lines from the corner pocket to the cushion nose in front of the diamonds as shown is very close to perfect (for 1/4 fraction use 1/2 diamond) – the red “v” near each diamond shows where the line would be for perfect fractions.
from Patrick Johson (in AZB post):
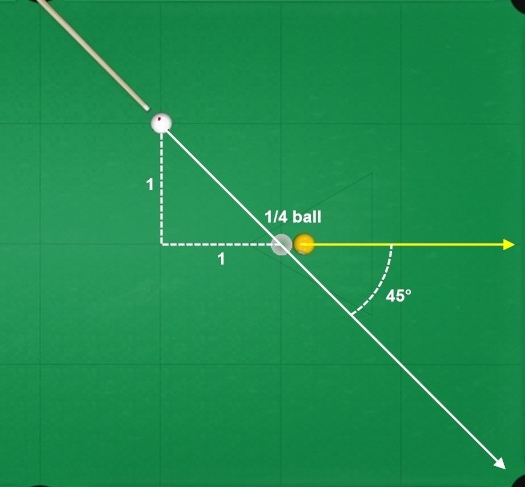
1-to-1 slope = 45-degree cut = 1/4 ball fraction
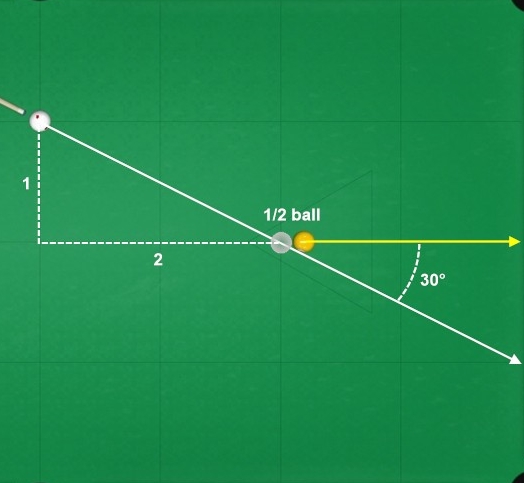
1-to-2 slope = ~30° cut = ~1/2 ball fraction
[Actual: 1.15-to-2 slope = 30° cut]
1-to-4 slope = ~15-degree cut = ~3/4 ball fraction
[Actual: 1.07-to-4 slope = 15° cut]
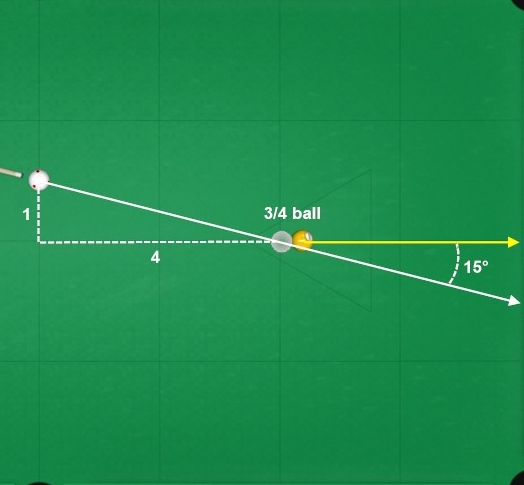
from Patrick Johnson (in AZB post and via e-mail):
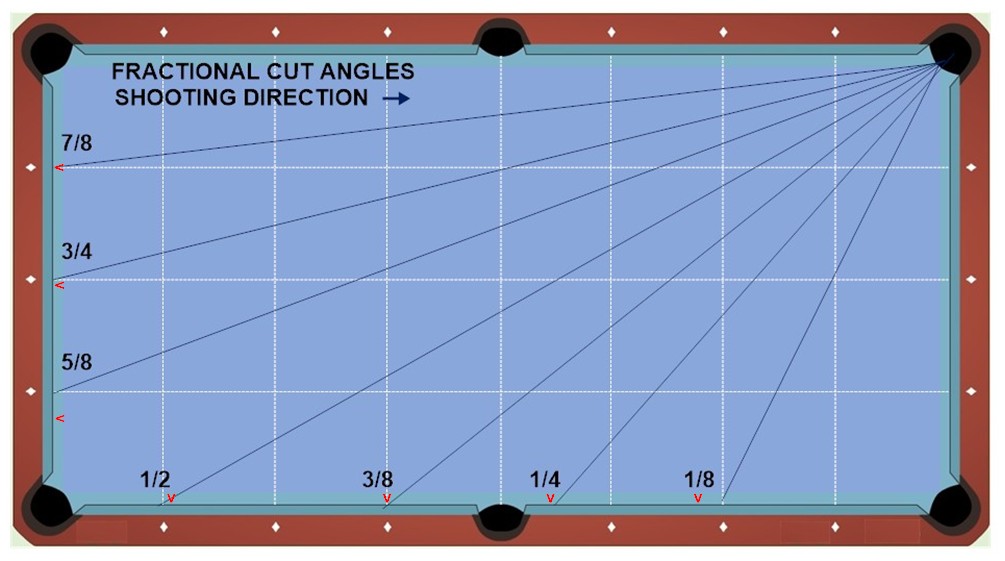
To use Fractions for aiming you need to get familiar with (learn to visualize at the table) the cut angles formed by the three common fractional overlaps: 3/4, 1/2 and 1/4 ball. To help with that, here’s a practice setup diagram of the fractional cut angles (left and right) for shots parallel with the short and long rails.
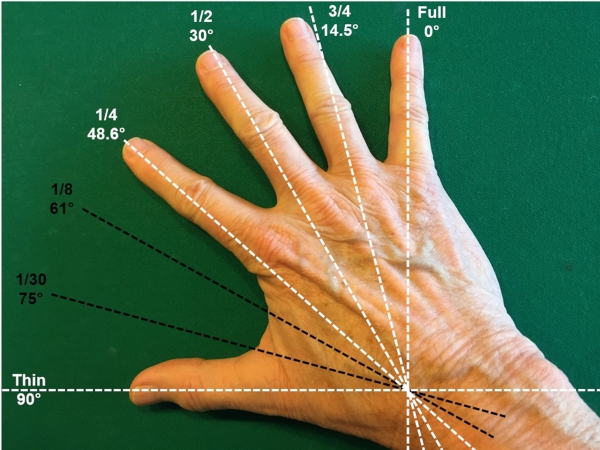
Your hand can be a useful guide for estimating the cut angles made by fractional CB/OB overlaps. Just spread your fingers as far as possible so the thumb and little finger form a 90° angle, and your other three fingers space themselves more of less naturally on the three major fractional cut angles (roughly 15, 30, and 45° – actual fractional cut angles shown below).
To cover the rest of the 90° “aiming field,” cut angles for two more (less frequently used) fractional overlaps are shown in black.
Use your other hand to estimate cuts in the other direction.
from Spiderman:
Like all “discrete”, “fractional-ball”, and similar aiming systems, it gets you in the ballpark for most shots and depends upon subconscious correction to make the fine adjustments. In other words, you have to use it as a guide, “take it on faith”, and shoot the shots.
For a beginner, it will get them in the ballpark and they’ll accidentally pocket more balls than by winging it. For an intermediate, they may have enough experience that they will subconsciously correct, and the system might work well for them. The expert doesn’t need a system to get them in the ballpark.
All discrete systems have the same failing – they are not geometrically correct for all setups. If you claim that there are only a (small) discrete number of aim points required to hit any pocket from any setup, and disallow the subconscious correction factor, all such systems may be easily disproven. In practice, your ability to compensate overcomes the built-in flaws of the system.
from Zafer Barutcuoglu (via June 2024 e-mails):
As an aid for developing my aim feel, I really like fractional-ball aiming over other methods. But estimating angles and then mapping to ball fractions isn’t easy, and seems unnecessary. I started using a simpler way, which surely has already been described in some Billiards Digest article decades ago: Observing that a cut angle’s sine is one minus the fractional-ball overlap ratio, we don’t need to estimate the angle itself at all. We can directly estimate the sine visually. For example:
Place the cue along the cut (OB direction) line, tip on the estimated ghost ball (GB) center, then rotate it around a fixed pivot point (e.g. the joint or the bumper) until perpendicular to the aim (CB-GB) line, and note the intersection point on the cue. The tip-to-intersection length as a fraction of the tip-to-pivot length is the fractional-ball overlap ratio. In other words, the intersection’s position between the tip and the pivot point is the aim point’s position between the OB center and a ball diameter away. Of course, using either the aim line or the cut line as the hypotenuse and dropping a perpendicular to the other works, or using their extensions over the OB for the reflected cut angle, but I like the above best because the cue starts where most people already place it to aim.
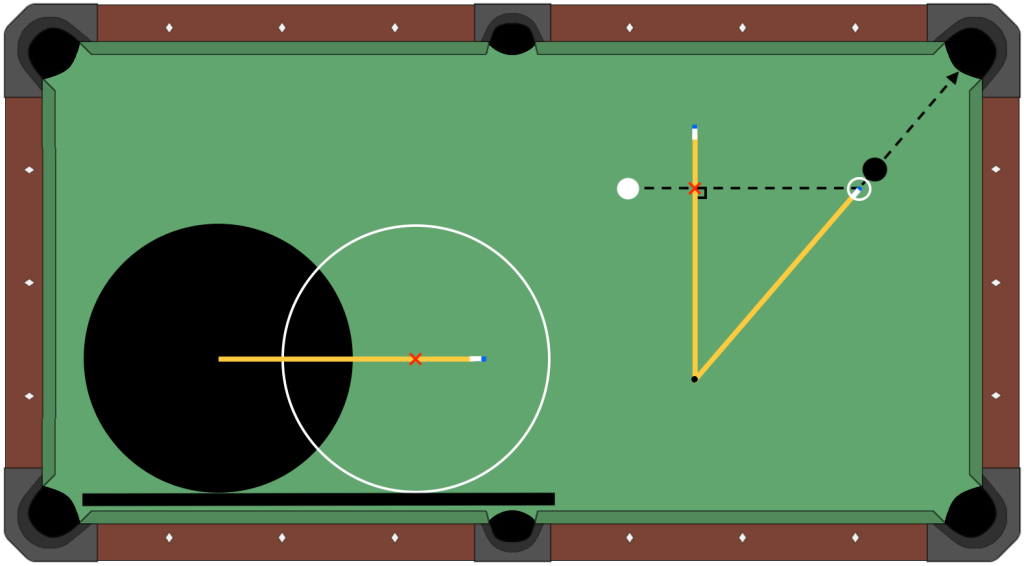
Another related tidbit, maybe a more personal crutch, but still one I wish I’d seen somewhere before it occurred to me, is using clock face points on the outside upper quadrant of the OB as fractional-ball aiming targets. Assuming cutting to the left (shooting to the right of the OB), with 3:00 being the half-ball hit, aiming at 1:00 (30º from top) is exactly a 3/4 ball hit, and easier for me aim at than visualizing the half radius inside the ball. Similarly, 12:30 (15º) is close to 7/8, 1:30 (45º) close to 5/8, and 2:00 not far from 7/16 for what it’s worth. For thinner than 1/2 ball hits, I visualize an imaginary tangent ball next to the OB (which is easy as it’s right next to a real ball) and aim at clock points on its inside upper quadrant. 9:00 is a half-ball hit, 11:00 is exactly the 1/4 ball, 11:30 is close to 1/8, 10:30 (45º) is about 3/8, and 10:00 isn’t far from 9/16.
Here’s a system for using the diamonds to approximate angles among the CB, OB, and pocket to determine the required throw-adjusted cut angle and and ball-hit fraction for any shot:
from Dr. Dave (related to the document linked above):
Here’s a March 2020 video demonstration from AimPro Billiards, showing how to use the diamonds to accurately estimate the cut angle for a shot.
Dr. Dave keeps this site commercial free, with no ads. If you appreciate the free resources, please consider making a one-time or monthly donation to show your support: