What is the difference between “sliding” and “rolling”, and can a ball “roll” when it has sidespin?
Good descriptions and demonstrations and “sliding” vs. “rolling” can be found here: cloth and cue ball effects. When a ball is sliding, drag action eventually converts bottom spin to stun and then to forward roll. Here’s a good demonstration of the effect:
And here’s an illustration (from Patrick Johnson) that shows how backspin gradually transforms to stun and then natural roll:
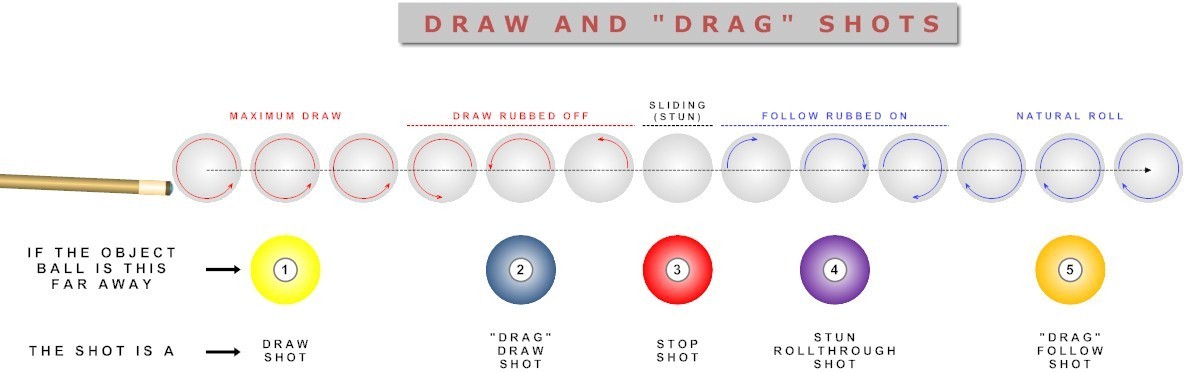
A ball starting out with pure sidespin and no top or bottom spin (i.e., stun) slides at first but immediately starts to develop forward roll due to sliding friction. See the spin axis “flip” demonstration for a good illustration of this. Once full roll develops, there is no longer any sliding. At that point, the ball continues to roll forward with sidespin. Both the forward speed and spin gradually slow due to rolling and spin resistance.
If a ball were rolling on an inked surface, the ink trace on the ball would be a circle. If the ball is rolling with no sidespin, the circle is vertical and goes around the full circumference (“great circle”) of the ball. If the ball is rolling with sidespin, the circle is smaller and tilted. With more sidespin and/or less forward speed, the circle is smaller and more tilted. A ball with lots of spin and very little forward roll would trace a very small circle. A ball spinning in place traces a point (the smallest possible circle). Every “rolling” ball traces a circle, and as the sidespin wears off, the circle size and tilt angle change.
See OB “swerve” and “turn” for an explanation and demonstrations of how and why a ball rolling with sidespin travels in a straight line.
There is often much confusion and misinterpretation about the various terms related to spin and english. Here’s a good summary of definitions:
- “roll” = “normal roll” = forward motion with the right amount of topspin to prevent sliding
- “sliding” = “stun” = translation with no topspin or bottom spin
- “overspin” = “extra topspin” = topspin faster than rolling rate
- “english” = “side” = sidespin
from Patrick Johnson (paraphrasing Mike Page):
Imagine that there’s a cylinder (like a barrel) exactly the right size so that it’s just contained within the ball. The cylinder/barrel’s top and bottom edges meet the ball’s surface like two latitude lines drawn around a globe in the northern and southern hemispheres.
Now imagine that you’ve tilted the barrel and are rolling it along the table’s surface like you’d roll a barrel on its edge. You can see that the axis of rotation is tilted, and the barrel’s bottom edge rolls along the table in a straight line without sliding at all.
Now imagine the ball surrounding the barrel rolling along with it across the table. This is how a ball rolls across the table with sidespin – no sliding, just rolling. If you were to put wet ink on the table it would mark a line around the ball at its “southern latitude” line.
The remaining wrinkle is that as the ball rolls its sidespin wears off and its axis of rotation becomes more and more horizontal. To visualize this, imagine that the tilted barrel within the ball tilts more and more onto its side, and simultaneously becomes fatter and fatter and shorter and shorter, but it continues rolling on its edge (you should be able to visualize doing this with a barrel that changes this way as you roll it). Eventually, when all the sidespin wears off, the fatter, shorter barrel becomes a flat disc rolling vertically on its edge. The wet ink line marked on the ball is actually a spiral that starts as a small tilted latitude and becomes a vertical “great circle” longitude when the ball is rolling normally without sidespin.
Can a cue ball have more topspin than the rolling amount right off the tip?
Yes, but not very easily. For more information (including demonstrations), see normal roll, maximum offset, and overspin.
Dr. Dave keeps this site commercial free, with no ads. If you appreciate the free resources, please consider making a one-time or monthly donation to show your support:
