Can an object ball swerve or turn due to sidespin?
First of all, OB “swerve” (OBS) or “turn” should not be confused with throw, which is an entirely different effect. In general, a ball can swerve (curve) only while it is sliding with a massé component of spin (although, see the info below). An object ball rolling with sidespin generally has no reason to turn, just like a CB rolling straight with sidespin (although, see the info below) . For an explanation and visualization of this, see slide and roll.
Here are some videos that demonstrate the lack of significant turn, which also apply to a CB rolling with sidespin (e.g., after any swerve has taken place):
A slight amount of “OB swerve” (most of which would be immediate swerve) is possible with massé spin transferred to the OB from follow or draw on the CB (see the end of TP A.24), but the effect is very small and of little practical importance (unless there is a large amount of throw due to cling/skid/kick). The videos above are instead looking at the effect of pure sidespin as a ball is rolling. This is called “OB turn.” The following video shows evidence for OB swerve in how apparent throw is greater with topspin vs. bottom spin shots, especially with cling:
Now, there is a “special” cue twisting and stroke swooping technique that can be used to swerve or turn an object ball, but it is quite controversial. Here’s a demonstration:
For more information, see the stroke swoop/swipe resource page.
Bob Jewett’s June ’92 BD article has an experiment you can use to test OB bending (or lack there of). Here’s the test from the article:
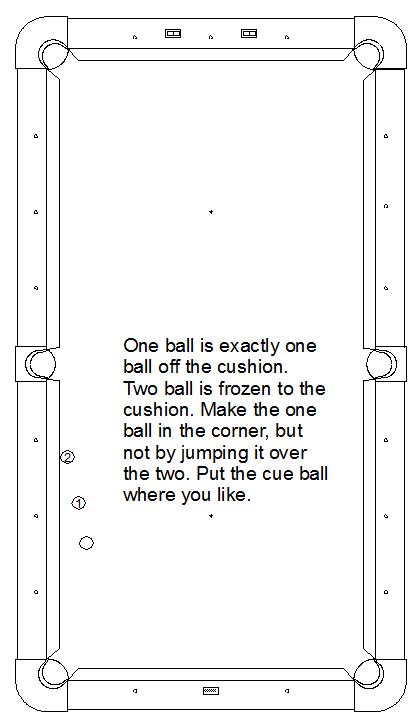
Here’s proof that OB swerve is possible; and with cling/skid/kick, it can be used to beat Bob Jewett’s Challenge above:
Online video NV B.7 (starting at the 2:49 point), offers an intuitive physical explanation for why a ball rolling with sidespin can turn. And TP B.2 provides a physics and math-based explanation. The analysis looks at the interaction of rolling resistance and spin resistance. Another theoretically possible effect is Magnus Effect curving (as with a baseball pitch, golf ball draw or fade, or bending soccer shot), but because pool balls are so smooth (unlike a baseball with raised stitches ,or a dimpled golf ball, or soccer ball seams) and because they travel relatively slowly over short distances (compared to the other examples) and because the magnitude of aerodynamic forces are so small compared to the weight of the ball (unlike with the other examples), and because the pool ball isn’t really spinning very fast compared to how fast it moving, the effect is negligible on a pool table. Here are the conclusions of the TP B.2 theoretical analysis: A ball rolling with sidespin goes straight for all practical purposes, and cloth irregularities or dirt (or slightly out-of-round or unbalanced balls) can create a much bigger effect, especially at slow speeds. Sometimes the ball will go straight as it slows with right spin, sometimes it will curve right as it slows with right spin, and sometimes it will curve left as it slows with right spin. Having said that, the physics does seem to suggest that there might be a small tendency for the ball to curve in the spin direction (e.g., right curve for right spin, the opposite direction as with the Magnus Effect), but due to the assumptions in the analysis and the results of the video demonstrations, the value of this information is questionable.
Although, a ball rolling slowly with a significant amount of sidespin can turn a noticeable amount, even on a level table. Ball turn can also occur if the ball is slightly out of round or is unbalanced (especially if the ball is spinning about an axis close to a bulge on the ball). Directional cloth weave, especially close to a pocket where the weave might be angled if the cloth was pulled tight during installation, can also influence ball turn, especially when the cloth is new. Dirt or cloth/slate irregularities on the table can also affect the ball’s path. Here’s an example of CB turn that ended a 434 straight-pool run by John Schmidt:
And here’s another:
Now, the CB can definitely be caused to curve with an elevated cue. For explanations and demonstrations, see squerve and massé shot aiming. The CB almost always swerves on sidespin shots because the cue is rarely level, since it needs to clear the rails (see cue elevation effects). Once a CB is done swerving (after any massé spin wears off), it rolls in a straight line with sidespin (except when it “turns”).
Here’s another example of ball turn on a directional, napped snooker cloth, where the direction of turn depends on the direction of the nap:
Can you explain the physics of OB swerve in simple terms?
Just think about CB swerve from a massé shot. To curve the CB to the left you need to hit down on the left side of the CB. To make the OB swerve to the left, you also need to hit down on the left side of the OB. This is accomplished with topspin on the CB with a cut to the right. The topspin transfers backspin to the OB in the line of centers direction; but because the OB is being thrown to the left, the backspin has a slight masse component. The detailed math and physics (with an illustration) can be found here:
TP A.24 – The effects of follow and draw on throw, and OB swerve
from Jal:
A ball with a massé spin component will change direction by the same amount regardless of how slick or “grabby” the cloth. But a more grabby cloth will cause that change of direction to happen sooner, so the curve will be tighter. In your example, a slicker cloth might be of some help since you want the 1-ball to execute a more open curve in order to clear the 2-ball.
However, an OB will not curve to any significant extent without being struck by an airborne cueball. That is, in order to induce a massé spin component, the cueball has to contact it above the horizontal equator. … this will also cause it to jump. The combination of jump and subsequent curve might be enough to clear the 2-ball and then “straighten out” after landing/bouncing and head for the pocket.
In principle, you can get the OB to curve just be using draw or follow at any non-zero cut angle. But calculations indicate that, at most, the change in direction is miniscule (in fact, very hard to measure and probably overridden by random buffeting by the cloth’s weave pattern).
dr_dave reply to Jal:
I agree 100%. OB swerve is not a significant-enough effect to be of any practical use. The effect is larger in clingy conditions, but still not significant enough to be useful or even noticeable.
The best chance to seemingly make an OB curve around an obstacle is by jumping the CB into the OB, creating OB hop over the obstacle ball, or by relying on table roll-off, a lopsided (non-round OB), or well-placed dirt or irregularities on the cloth. The rail groove can also influence an OB close to the cushion. Even the magical cue twist and swoop technique won’t work (without a weighted ball).
Dr. Dave keeps this site commercial free, with no ads. If you appreciate the free resources, please consider making a one-time or monthly donation to show your support:
